This week's article was "Creating a Differentiated Mathematics Classroom," and since our district has been on a journey to differentiated instruction during the past three years, I am always on the lookout for DI ideas specific to math.
I've had a lot of professional development on DI, and I'm in the Dr. Carol Ann Tomlinson fan club, so if you're not familiar with the tenets of differentiated instruction, here's a quick summary of what I know...
The principles of DI include high quality curriculum, ongoing assessment, *instruction that responds to student variance, all working within a classroom community. (Dr. Tomlinson's latest edition of The Differentiated Classroom has changed a bit of the wording. When we first learned about DI, we separated *this tenet into flexible grouping and respectful tasks.) Teachers can differentiate through content, process, and product, all according to the student's readiness, interests, and learning profile.
In addition, differentiation by interest increases student motivation, differentiation by readiness produces growth, and differentiation by learning profile improves efficiency.
As as a math teacher, the "easiest" way for me to understand differentiation was by student readiness. I thought, "Sure, I can do a quick assessment to see where my students are struggling," and respond to their needs. (That only took two years, and I'm definitely not an expert, but I have a growth mindset about learning about assessment!) I'm still working on writing awesome pre-assessments for my students, though...that is a real challenge for me!
I struggled with understanding learning profile, but the first thing I tried was to have my students assess themselves on their intelligence type. (They learned a tiny bit about Gardner's Multiple Intelligences, they completed a survey and responded on a Google form, so then I had a record of their personal assessments.) I created seating charts and groups based on their preferred intelligence, and they enjoyed sitting with like-minded students, but I didn't do much else with that grouping. (sad face)
This year, I tried an additional activity to use learning profile, and it was moderately successful. In recent trainings, I enjoyed "CAP" activities, so that's what I tried to duplicate for math...but I only did this one time. (another sad face!) I talked my students through the creative-analytical-practical descriptions of Sternberg's Theory of Intelligence, and they quickly self-assessed their intelligence on this Google form.
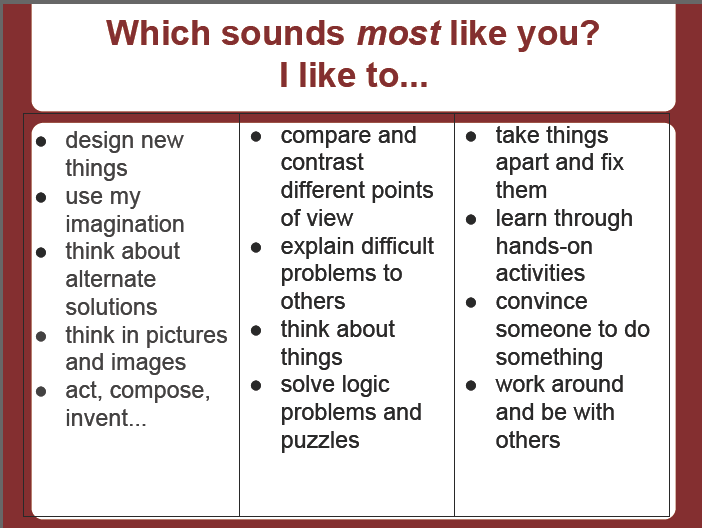 |
| Column 1: Creative; Column 2: Analytical; Column 3: Practical |
My students divided into their C-A-P groups, and they had the remainder of the period to work on this assignment. We were creating and solving sinusoidal models, and I originally thought this type of assignment was general enough that it could be used with a variety of future lessons. (Sigh. Perhaps if I had been faithful about blogging, I would have returned to this idea!)
I guess the bottom line is to know your students, craft lessons based on their needs, and be purposeful about students' work and assessments. (Whew, is that all???) I'm looking forward to the #eduread chat to help solidify my thinking about differentiation and learning profiles in mathematics!
A few of my summer educational reads...
- The Differentiated Classroom: Responding to the Needs of All Learners (2nd edition), Carol Ann Tomlinson
- Trust Matters: Leadership for Successful Schools (2nd edition), Megan Tschannen-Moran
- Instructional Rounds in Education: A Networked Approach to Improving Teaching and Learning, City, Elmore, Fiarman and Teitel
- Leaders Eat Last, Simon Sinek
- Quiet: The Power of Introverts in a World That Can't Stop Talking, Susan Cain
- (re-read) Teach Like a Pirate, Dave Burgess


